Details

Written by Tsirha Adefris

DISCUSSION

1. Darwin on Natural Selection and Extinction

Charles Darwin (1859) made much more than a brief mention on the evolutionary process of extinction. The point made that relates to this thesis is that Darwin stated that Natural Selection, the process that has continued to gain popularity and acceptance, is intimately related with extinction. He relegated the study of extinction to the examination of geological processes where it presently resides (Lister, 2011). 

           

Variation

The theses of Origins (Darwin, 1959) begins with detailed background references to both variation under domestication and under nature. It is evident that variation forms the substrate for NS and EX. Darwin’s discussion presents a foreword on variation under domestication as manipulated by the breeder and variation as it occurs in nature. The choice of variants by the breeder has been termed “artificial” selection thus lending the term for what occurs in nature (NS). It is apparent from his description that both the breeder and nature “favor” certain variants. It follows that the variants that fall out of favor are relegated to extinction under nature. In the absence of an exact definition of the manner of inheritance and the failure of an inference to on the nature of species Darwin’s speculations on variation contribute to his work on breeding finches and his seminal work on the adaptive radiation of the Galapagos Finches mentioned as an aside. 

Darwin’s ideas on variation, heredity, and development differ significantly from twentieth-century views. First, Darwin held that environmental changes, acting either on the reproductive organs or the body, were necessary to generate variation. Second, heredity was a developmental, not a transmission, process; variation was a change in the developmental process of change. (Winther, 2000)

Darwin’s reference to experiments in breeding are lacking due to the absence of an operational definition of inheritance.

Darwin's theory of natural selection lacked an adequate account of inheritance, making it logically incomplete. The interaction between evolution and genetics, shows how, unlike Mendel, Darwin's lack of a model of the mechanism of inheritance left him unable to interpret his own data that showed Mendelian ratios, even though he shared with Mendel a more mathematical and probabilistic outlook than most biologists of his time. Darwin's own “pangenesis” model provided a mechanism for generating ample variability on which selection could act. Pangenesis in essence, Darwin borrowed from Lamarck and he referred to it repeatedly in Origins as “the principle of use and disuse. ”It involved, however, the inheritance of characters acquired during an organism's life, which Darwin himself knew could not explain some evolutionary situations, but has  more currently become considered operational. (Liu, 2013).  

Once the particulate basis of genetics was understood, it was seen to allow variation to be passed intact to new generations, and evolution could then be understood as a process of changes in the frequencies of stable variants. Evolutionary genetics subsequently developed as a central part of biology. Darwinian principles now play a greater role in biology than ever before, which we illustrate with some examples of studies of natural selection that use DNA sequence data and with some recent advances in answering questions first asked by Darwin. (Charlesworth & Charlesworth, 2009)

Ever since, with the tools of genetics theory, the “Breeder’s Equation” has been formulated which demonstrates the NS and EX components in breeding,

Breeder’s Equation = Delta Z = h2S (Lush, 1937)

Delta Z = Change in mean value of trait, h2 = heritability, S = selection differential

S is -ve if lower trait values confer increased survival

S is +ve if Selection favors higher trait values.

S represents the relationship between phenotypic values and fitness.

As such, +S is NS and -S is EX.

 

            Competition

The Origin’s (1859) chapter on The Struggle for Existence reveals the unity of NS and EX. Evolutionary game theory as demonstrated by the Hawks-Dove game may find an application here. (Smith J. M., 1986). Darwin himself utilized a predator -prey model to illustrate natural selection.

As Went (1973) characterizes competition, he suggests that in the Darwinian theory competition has taken on additional meanings in relation to struggle for existence. Competition was not anymore, “a struggle between equals, but a mechanism to award superiority. Competition became a contest, and considerations of combat, struggle, territorial exclusion, and even war entered in the wake of Darwin's ideas.” (Went, 1973)

It is fairly well known that Darwin was inspired to formulate his theory of natural selection by reading Thomas Malthus’s Essay on the Principle of Population. In fact, by reading Darwin’s notebooks, we can even locate one particular sentence which started Darwin thinking about population and selection. What has not been done before is to explain exactly where this sentence – essentially Malthus’s ideas about geometric population growth came from an 18^th Century mathematician Leonard Euler. (Klyve, 2014)

The Darwinian perspective on competition and its role in evolution has best been presented in a summary statistic that contrasts it with speciation. Extinction is thus described as competition – mediated. Extinct taxa, as stated by Rabosky (2013) have failed to speciate at macroevolutionary scales. Rabosky’s (2013) model that does not require a zero - sum game is summed up with the equation for the speciation rate as a function of current species richness (n), the theoretical diversity limit (K_MAX), and a new parameter S₀ that describes the baseline rate of speciation in the absence of diversity-dependence:

An equivalent function can be written for extinction, with the addition of two parameters: E₀, the extinction rate in the absence of diversity-dependence, and ω, the linear effect of diversity on extinction. The overall extinction rate is

 

Adaptation

Adaptation is regarded as a driving force in natural selection. The term adaptation was coined by Bishop William Paley in his Watchmaker Analogy, where he argued that each creation is adaptively designed by a creator. (McGrath, 2011). Darwin did not follow the natural Theology of Bishop Usher. Darwin focused on competition while laying out the manner of selection. His reference to adaptation is summed up in the statement in Origins (171) where he ascribes the concept of adaptation to Cuvier. Darwin accepts adaptation as borrowed from Cuvier to be closely linked with natural selection. He relates that natural selection adapts organs to their conditions of life at all periods.

“On my theory, unity of type is explained by unity of descent. The expression of conditions of existence, so often insisted upon by the illustrious Cuvier, is fully embraced by the principle of natural selection. For natural selection acts by either now adapting the varying parts of each being to its organic and inorganic conditions of life or by having adapted them during long-past periods of time.”

Adaptation, which he names “the Laws of the Conditions of Life”, he considers the higher law to the “Law of the Unity of Type”. The latter law being explained by Darwin as the fundamental agreement in structure of organic beings independent of their habits of life. The environment is the condition whereby the selective process operates.

Adaptive radiation is as much or a more important contribution by Charles Darwin than natural selection. Darwin’s views on adaptation were formed through his work as a naturalist where he noted species with a common ancestor adapting to different environmental conditions. Many of Darwin’s experiences on his trip aboard the HMS Beagle shaped his thinking. The most influential of these is the time he spent in the Galapagos Islands. Geographic isolation and adaptive radiation are the lessons learned from the distribution of related groups of birds on The Galapagos islands. (Losos & Ricklefs, 2009)

 

 

Orr and Unckless (2008) discuss that theories of adaptation typically ignore the effect of environmental change on population size. But some environmental challenges—challenges to which populations must adapt—may depress absolute fitness, causing populations to decline. Under this scenario, adaptation is a race; beneficial alleles that adapt a population to the new environment must sweep to high frequency before the population becomes extinct. We derive simple, though approximate, solutions to the probability of successful adaptation (population survival) when adaptation involves new mutations, the standing genetic variation, or a mixture of the two. Our results show that adaptation to such environmental challenges can be difficult when relying on new mutations at one or a few loci, and populations will often decline to extinction. (Orr, Unckless 2008)

We recommend opening this source in your browser. If you copy and paste from there, remember to add citations in Word.

 

Hammerstein (1996) has also concluded that long-term stable state can be characterized at the phenotypic level as a fitness maximum, a Nash equilibrium or an Evolutionary Stable State.

 

Biktashev (2014) describes a simple mathematical model of gradual Darwinian evolution in continuous time and continuous trait space, due to intraspecific competition for common resource in an asexually reproducing population in constant environment, while far from evolutionary such a stable equilibrium.

 

 

One of the simplest models of adaptation to a new environment is Fisher’s Geometric Model (FGM), in which populations move on a multidimensional landscape defined by the traits under selection. The predictions of this model have been found to be consistent with current observations of patterns of fitness increase in experimentally evolved populations. Recent studies investigated the dynamics of allele frequency change along adaptation of microbes to simple laboratory conditions and unveiled a dramatic pattern of competition between cohorts of mutations, i.e., multiple mutations simultaneously segregating and ultimately reaching fixation. Here, using simulations, we study the dynamics of phenotypic and genetic change as asexual populations under clonal interference climb a Fisherian landscape, and ask about the conditions under which FGM can display the simultaneous increase and fixation of multiple mutations—mutation cohorts—along the adaptive walk. We find that FGM under clonal interference, and with varying levels of pleiotropy, can reproduce the experimentally observed competition between different cohorts of mutations, some of which have a high probability of fixation along the adaptive walk. Overall, our results show that the surprising dynamics of mutation cohorts recently observed during experimental adaptation of microbial populations can be expected under one of the oldest and simplest theoretical models of adaptation—FGM. (Sousa, Alpedrinha, Campos, & Gordo, 2016)

 

Populations subject to substantial environmental stress, such as occurs during colonization attempts, human-mediated introductions or reintroductions, or global climatic change, may face a risk of extinction. There are many examples of such extinctions, but many examples are known in which populations have evolved sufficiently to persist in changed environments, such as cases of evolved resistance to pesticides or heavy metal toxins. An important problem for evolutionary biologists is thus to characterize those combinations of genetic and demographic conditions likely to result in persistence versus those expected to lead to extinction in a changed environment. Theoretical work has characterized circumstances in which populations have sufficient genetic capacity to avoid extinction by adapting with sufficient speed to a continuously changing environment (Pease et al. 1989; Lynch et al. 1991; Lynch and Lande 1993; Burger and Lynch 1994). A model used to highlight an additional risk faced even by populations genetically capable of evolving sufficiently to persist in environments that remain constant following a single, initial abrupt change. Namely, as a population adapts to a novel environment, its density may fall below a critically low level for a period of time, during which the population is highly vulnerable to extinction by demographic stochasticity. If this occurs, the population is likely to vanish before it can be rescued by evolution. To examine this problem, a population dynamic and an evolution by natural selection model were coupled to identify conditions for which evolution succeeds-or fails-to rescue a closed population from extinction following abrupt environmental change. The models considered here cover extremes in both genetics (one-locus and polygenic models) and population growth (discrete and continuous-time models). These models lead to a similar conclusion: even populations with the genetic wherewithal to potentially persist in a novel environment may often fail to do so. Moreover, our analyses help to quantitatively characterize situations in which evolution by natural selection can effectively rescue a population from impending extinction. We suspect the qualitative properties of our results may be general features of evolutionary dynamics in novel environments. (Gomulkiewicz & Holt, 1995)

 

 

The Genetic Theory of Natural Selection

 

Fisher’s law of natural selection is stated as: ‘The rate of increase in the mean fitness of any organism at any time ascribable to natural selection acting through changes in gene frequencies is exactly equal to its genic variance in fitness at that time’.

 

‘I attempted mathematics, and even went during the summer of 1828 with a private tutor (a very dull man) to Barmouth, but I got on very slowly. The work was repugnant to me, chiefly from my not being able to see any meaning in the early steps in algebra. This impatience was very foolish, and in after years I have deeply regretted that I did not proceed far enough at least to understand something of the great leading principles of mathematics; for men thus endowed seem to have an extra sense’ (Grafen, 2003)

Admittedly the genius of Darwin by his own admission falls short of the mathematical and his theory had to await the discovery of mendelian genetics and the formulation of the genetic theory by Ronald Fisher.

Fisher’s theorem has been revised by Price (Gardner, 2008)

The Price equation and Fisher's Fundamental theory of Natural selection are mathematical expressions of change in gene frequency over time, modeling natural selection. Gardner (2008) has remarked that eq.1 approximates Darwin's idea of "Survival of the fittest". This equation also directly approximates extinction and is further proof that natural selection as conceived by Darwin is translatable to extinction

To paraphrase Fisher’s theorem here, “the variance in fitness is equal to the differential reproductive fitness at the particular time”.

                                                                                W = d M / d t                                                            eq. 1

 

Where

W= genetic variance in fitness

M= mean fitness

t= time

 

Fisher regarded fitness to improve over time.  Price’s modification of the theorem gives the equation for selection and has still not made allowance for coefficient of fitness (1-w)

 

                                                                                R = Cov (w,g)

 

R is response to selection and equal to the mean of the change in character value (Z)

Z = g+e

w is fitness

g is character value

e is unexplained character value

 

The suggested response to evolutionary drive takes the change in character as E and the equation for covariance will include w, fitness (leading to selection) and 1-w (coefficient of selection, leading to extinction.

 

                                                                                E = Cov (w, 1-w)

 

 

Also, Fisher’s definition of genetic variance uses a metric that changes with the population, thus his measure of genetic fitness is only applicable to a single moment in time, thwarting the development of a dynamic model of the evolution of the population (Price 1972; Ewens 1989). Fisher defines the expected value of fitness of an organism y to be

X(y)=m¯+∑lQl,a(y,l)

1.1

where m¯ is the average fitness of the population, the sum is over every loci l in the genome, a(y, l) is the allele for the organism y at loci l, and Q_l,a is the “increment” [Fisher’s terminology (Fisher 1930, p. 32)] associated with allele a at loci l, defined by Fisher to be the difference from the mean fitness that an organism will gain by having this allele at this locus. While Fisher does not provide a direct formula for the increments, Price (1972) suggests that they are the regression coefficients associated with the allele, defined by letting P_l,a be the population of all organisms with allele a at locus l, #P_l,a be the number of organisms in population P_l,a, m(y) be the fitness of organism y, m¯ be the mean fitness of the total population, and

Ql,a=∑y∈Pl,am(y)−m¯#Pl,a.

1.2

The genetic variance as defined by Fisher is the variance of the genetic fitness X(y) over all organisms y [See Price (1972) for a complete derivation from this perspective]. Because Fisher’s measure of genetic fitness of each organism y depends on the constituency of the population as a whole at that time, his theorem cannot be extended to a dynamic model over time.

This evolutionary scenario only results in a minor increase in fitness followed by terminal stasis. Apart from a constant supply of new mutations, Fisher’s Theorem would actually suggest that “Mendelism has killed Darwinism” (Glick 2009, p. 265), a common view in Fisher’s time. This is precisely the opposite of what Fisher wanted to prove.

 

The extinction of small populations is a stochastic process, affected by both environmental variation and chance variation in the fates of individuals (demographic stochasticity). Fox (2005) has examined how population extinction risk is affected by variation in the underlying individual phenotypes, using a branching-process approach. Long-term individual extinction risk as the chance of ultimately leaving no descendants, and the cumulative individual extinction risk as the chance of leaving no descendants by a specified time has been examined. These show that if there is a phenotypic correlation between parents and their offspring, variation in these quantities always reduces both the long- and short-term population extinction risk. Such variation in individual extinction risk arises from individual variation in demographic parameters and may have both genetic and environmental causes. Using a well-known approximation of the difference between the log arithmetic and log geometric means, expressions for the sensitivity and elasticity of the approximate log extinction risk to changes in the mean and variance of the individual extinction risk, and to changes in population size have been derived. One conclusion is that increasing the variance among individuals in extinction risk can sometimes be at least as important in reducing population extinction risk as increasing the population size itself. These analyses also point to reasons why changes in environmental factors (e.g., toxicants) or management practices may have either larger or smaller effects than would be anticipated by considering the change in the mean risk alone. (Fox, 2005)

Mousseau and Roff (1987) tested the hypothesis that traits closely associated with fitness will generally possess lower heritability than traits more loosely connected with fitness was tested using 1120 narrow sense heritability estimates for wild, outbred animal populations, collected from the published record. Results indicate that life history traits generally possess lower heritability than morphological traits, and that the means, medians, and cumulative frequency distributions of behavioral and physiological traits are intermediate between life history and morphological traits. The findings are consistent with popular interpretations of Fisher's (1930, 1958) Fundamental Theorem of Natural Selection, and Falconer (1960, 1981), but also indicate that high heritability is maintained within natural populations even for traits believed to be under strong selection. It is also found that the heritability of morphological traits is significantly lower for ectotherms than it is for endotherms which may in part be a result of the strong correlation between life history and body size for many ectotherms. (Moussea, Roff 1987)

 

The problem of interpreting negative maximum likelihood estimates of heritability that sometimes arise from popular statistical models of additive genetic variation was considered by Steinsaltz et.al (2020). These may result from random noise acting on estimates of genuinely positive heritability, but it is argued that they may also arise from misspecification of the standard additive mechanism that is supposed to justify the statistical procedure. Researchers should be open to the possibility that negative heritability estimates could reflect a real physical feature of the biological process from which the data were sampled (Steinsaltz et.al. 2020)

 

Because of the ubiquity of genetic variation for quantitative traits, virtually all populations have some capacity to respond evolutionarily to selective challenges. However, natural selection imposes demographic costs on a population, and if these costs are sufficiently large, the likelihood of extinction will be high. We consider how the mean time to extinction depends on selective pressures (rate and stochasticity of environmental change, and strength of selection), population parameters (carrying capacity, and reproductive capacity), and genetics (rate of polygenic mutation). We assume that in a randomly mating, finite population subject to density-dependent population growth, individual fitness is determined by a single quantitative-genetic character under Gaussian stabilizing selection with the optimum phenotype exhibiting directional change, or random fluctuations, or both. The quantitative trait is determined by a finite number of freely recombining, mutationally equivalent, additive loci. The dynamics of evolution and extinction are investigated, assuming that the population is initially under mutation-selection-drift balance. Under this model, in a directionally changing environment, the mean phenotype lags behind the optimum, but on the average evolves parallel to it. The magnitude of the lag determines the vulnerability to extinction. In finite populations, stochastic variation in the genetic variance can be quite pronounced, and bottlenecks in the genetic variance temporarily can impair the population's adaptive capacity enough to cause extinction when it would otherwise be unlikely in an effectively infinite population. We find that maximum sustainable rates of evolution or, equivalently, critical rates of environmental change, may be considerably less than 10% of a phenotypic standard deviation per generation. (Burger and Lynch 1995)

 

The general theories of molecular evolution depend on relatively arbitrary assumptions about the relative distribution and rate of advantageous, deleterious, neutral, and nearly neutral mutations. The Fisher geometrical model (FGM) has been used to make distributions of mutations biologically interpretable. The FGM-based molecular model was explored to represent molecular evolutionary processes typically studied by nearly neutral and selection models, but in which distributions and relative rates of mutations with different selection coefficients are a consequence of biologically interpretable parameters, such as the average size of the phenotypic effect of mutations and the number of traits (complexity) of organisms. A variant of the FGM-based model that was called the static regime (SR) represents evolution as a nearly neutral process in which substitution rates are determined by a dynamic substitution process in which the population's phenotype remains around a suboptimum equilibrium fitness produced by a balance between slightly deleterious and slightly advantageous compensatory substitutions. As in previous nearly neutral models, the SR predicts a negative relationship between molecular evolutionary rate and population size; however, SR does not have the unrealistic properties of previous nearly neutral models such as the narrow window of selection advantageous compensatory substitutions. As in previous nearly neutral models, the SR predicts a negative relationship between molecular evolutionary rate and population size; however, SR does not have the unrealistic properties of previous nearly neutral models such as the narrow window of selection strengths in which they work. In addition, the SR suggests that compensatory mutations cannot explain the high rate of fixations driven by positive selection currently found in DNA sequences, contrary to what has been previously suggested. We also developed a generalization of SR in which the optimum phenotype can change stochastically due to environmental or physiological shifts, which we called the variable regime (VR). VR models evolution as an interplay between adaptive processes and nearly neutral steady-state processes. When strong environmental fluctuations are incorporated, the process becomes a selection model in which evolutionary rate does not depend on population size, but is critically dependent on the complexity of organisms and mutation size. strengths in which they work. In addition, the SR suggests that compensatory mutations cannot explain the high rate of fixations driven by positive selection currently found in DNA sequences, contrary to what has been previously suggested. We also developed a generalization of SR in which the optimum phenotype can change stochastically due to environmental or physiological shifts, which we called the variable regime (VR). VR models evolution as an interplay between adaptive processes and nearly neutral steady-state processes. When strong environmental fluctuations are incorporated, the process becomes a selection model in which evolutionary rate does not depend on population size but is critically dependent on the complexity of organisms and mutation size. For SR as well as VR we found that key parameters of molecular evolution are linked by biological factors, and we showed that they cannot be fixed independently by arbitrary criteria, as has usually been assumed in previous molecular evolutionary models. (Razeto-Barry, Díaz, & Vásquez, 2012)

In 1927, Fisher suggested that Mullerian mimicry evolution could be gradual and driven by predator generalization. A competing possibility is the so-called two-step hypothesis, entailing that Mullerian mimicry evolves through major mutational leaps of a less-protected species towards a better-protected, which sets the stage for coevolutionary fine-tuning of mimicry. At present, this hypothesis seems to be more widely accepted than Fisher's suggestion. We conducted individual-based simulations of communities with predators and two prey types to assess the possibility of Fisher's process leading to a common prey appearance. It was found that Fisher's process worked for initially relatively similar appearances. Moreover, by introducing a predator spectrum consisting of several predator types with different ranges of generalization, we found that gradual evolution towards mimicry occurred also for large initial differences in prey appearance. We suggest that Fisher's process together with a predator spectrum is a realistic alternative to the two-step hypothesis and, furthermore, it has fewer problems with purifying selection. We also examined the factors influencing gradual evolution towards mimicry and found that not only the relative benefits from mimicry but also the mutational schemes of the prey types matter. (Balogh & Leimar, 2005)

 

The Fossil Record

 

The fossil record is a firm confirmation of extinction events forming a considerable length of earth history.

We can also learn about evolutionary changes that may be ascribable to natural selection from the fossil record.

The formula for the extinction rate from paleontology is = (A conservative estimate of background extinction rate for all vertebrate animals is 2 E/MSY, or 2 extinctions per 10,000 species per 100 years.) 

 

Whereas an evolutionary rate in the unit darwin is = The darwin (d) is a unit of evolutionary change, defined by J. B. S. Haldane in 1949. One darwin is defined to be an e-fold (about 2.718) change in a trait over one million years. Haldane named the unit after Charles Darwin.

 

The darwin r is calculated from changes in the dimensions of fossils as such r = lx2-lx1 / Delta t where lx2, and lx1 are final and initial value of trait and t is time.

 

The evolutionary rate calculation relates to selection of traits coupled when coupled with the extinction rate, the selection process translates into the extinction of species.

  

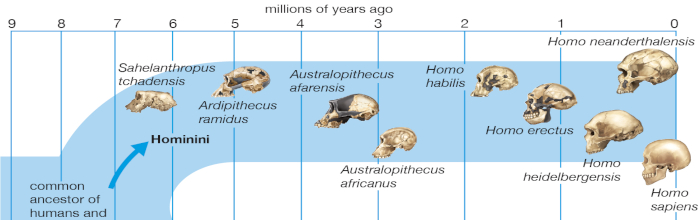
Hominid fossils predating the emergence of Australopithecus have been sparse and fragmentary. The evolution of our lineage after the last common ancestor we shared with chimpanzees has therefore remained unclear. Ardipithecus ramidus, recovered in ecologically and temporally resolved contexts in Ethiopia’s Afar Rift, now illuminates earlier hominid paleobiology and aspects of extant African ape evolution. More than 110 specimens recovered from 4.4-million-year-old sediments include a partial skeleton with much of the skull, hands, feet, limbs, and pelvis. This hominid combined arboreal palmigrade clambering and careful climbing with a form of terrestrial bipedality more primitive than that of Australopithecus. Ar. ramidus had a reduced canine/premolar complex and a little-derived cranial morphology and consumed a predominantly C 3 plant–based diet (plants using the C 3 photosynthetic pathway). Its ecological habitat appears to have been largely woodland-focused. Ar. ramidus lacks any characters typical of suspension, vertical climbing, or knuckle-walking. Ar. ramidus indicates that despite the genetic similarities of living humans and chimpanzees, the ancestor we last shared probably differed substantially from any extant African ape. Hominids and extant African apes have each become highly specialized through very different evolutionary pathways. This evidence also illuminates the origins of orthogrady, bipedality, ecology, diet, and social behavior in earliest Hominidae and helps to define the basal hominid adaptation, thereby accentuating the derived nature of Australopithecus. (White, et al., 2009)

The distribution of the Hominini over time and space is evidence that selective processes were vigorous at each taxonomic level resulting in an extinction turnover process over the period of the evolution leading to humanity.

 

 

 

Endemism

 

Patterns of species diversity on islands have yielded significant insights into evolutionary and ecological processes such as immigration, speciation and extinction. Endemism is but the final point a species reaches after its origination and diversification. It is but a general rule that most species are driven to extinction. Speciation has been considered as a primary process contributing to species diversity, but its contribution to the diversity of local communities has not been fully appreciated. Based on the theory of classic island biogeography, we derived a model for the number of endemic species as a function of the processes of immigration, speciation, and extinction. The model shows that species endemism on an island is proportional to speciation rate but decreases with the sum of immigration and extinction rates (i.e., the species turnover rate). The model predicts that the contribution of immigration to species richness in local communities decreases with time, while the contribution of speciation to local richness increases with time. It further shows that only when the speciation rate is larger than half of the extinction rate can new species added from speciation eventually surpass those added from immigration. We conclude that, although the model leads to an apparent positive relationship between percentage endemism and species diversity on an island, this positive endemic–diversity relationship is not necessarily driven by speciation. (Chen & He, 2009)

A species during its history undergoes a selective process coupled with directional extinction in the background suggested to be termed devolution. Island species richness and endemism are salient parameters for biologists and conservationists, yet in the voluminous works on island biogeography, the relationship between richness and endemism has not been thoroughly explored. Island biogeography theory suggests that both the species richness of a given island and the percentage of species that are endemic to that island are functions of the island’s physical properties and its degree of isolation (MacArthur and Wilson 1967, p. 173). In separate analyses of the floras and arthropod faunas of the Hawaiian and Canary island archipelagos, Emerson and Kolm (2005a) found that species richness was a better predictor of percent endemism than were island size, island age, maximum island height, or distance to nearest neighboring island. On the basis of this result, they inferred that species richness was causing accelerated speciation. However, Emerson and Kolm did not fully consider alternative interpretations, particularly those that do not invoke differences in island-specific rates of speciation. For example, it is possible that diversity and endemism might be linked under a simple null model of island community assembly. In this paper, we demonstrate that a positive correlation between diversity and endemism is an expected outcome of island colonization, and that intrinsic variation among species and islands can amplify the magnitude of that correlation. Consider the following two lists, L1 and L2, that differ in length such that L1! L2.  from Witt and Maliaikal-Witt( 2007) (A number of elements, S, are shared between the two lists, while the remainder are unique to one list or the other. The proportion unique to each list is: U i " (L i # S)=L i " 1! S=L i It follows that the longer list (island with greater species richness), L1, will always have a higher proportion unique (L1! L2). This is a tautological property that applies to any pair of lists that share some elements. We suggest that it is also true for any set of N lists. In a simple incidence matrix for S species (rows) in N samples (columns, species lists) where the total number of incidences varies among samples (i.e. species lists vary in richness) and some species are shared among some or all samples, the larger samples will tend to have a greater proportion unique than the smaller ones. We cannot envision a non-random arrangement of incidences among columns that could overcome this expected correlation. Correspondingly, in any set of communities that contains some shared species, more diverse communities will contain a higher proportion of endemic species. Jetz et al. (2004) recognized this phenomenon in an analysis of richness and endemism in the continental African avifauna and corrected for it using a null model. The same principle applies to the colonization of island archipelagos from a finite continental pool of potential colonist species (an infinite pool could eliminate sharing of species between islands). Correspondingly, a stochastic colonization process should cause more diverse islands to contain proportionately more single-island endemic species. To further demonstrate this point, we used the Hawaiian arthropod dataset (Nishida 2002) that was also used by Emerson and Kolm (2005a). This dataset includes 8068 species on 17 islands, comprising 16623 island population. (Witt & Maliakal-Witt, 2007)

Biber (2002) examined the relationship between island biogeography and the vulnerability of island biota to extinction as a result of human activities was examined. In particular, this study analyzed whether island area, maximum elevation of an island, isolation from the nearest continental landmass, or date of human colonization had statistically significant relationships with the proportion of endemic island bird species that have become endangered or extinct. The study examined islands or island groups with endemic bird species, and which have never been connected to a continental landmass. Both modern and fossil bird species were incorporated into the analysis. Islands that were colonized by humans earliest had the lowest proportion of modern species alone, and modern and fossil species combined, that have gone extinct. However, date of human arrival was not correlated with the proportion of modern species that are endangered. Maximum elevation of an island was negatively correlated with the proportion of modern species that are extinct and was positively correlated with the proportion of modern species that are endangered. Area was negatively correlated with the proportion of modern species that are endangered. Isolation of islands was not significantly correlated with the proportion of modern species extinct or endangered but was positively correlated with the proportion of modern and fossil species combined that have gone extinct. These results indicate that the initial spasm of island bird extinctions due to human contact may have, in part, passed. They also indicate that bird species on islands colonized earliest by humans may have had more time to adapt to the presence of man and his commensal species, resulting in reduced extinction rates. (Biber, 2002)

The following discussion is an excellent example of an appearance of a neoendemic from ancestral species under variable environments. Abstract Divergent selection on ecological traits is thought to be the main driver of ecological speciation, leading directly or indirectly to the evolution of reproductive barriers between populations in different environments without geographic isolation. Low competition in stressful habitats as well as habitat heterogeneity occurring between biotic regimes are factors, which actively promote speciation in higher plants. The relatively young landscape of the Elbe estuary (Northern Germany) provides an excellent opportunity for studying ecological differentiation in species colonizing the newly developing marshes during the postglacial period. Deschampsia wibeliana (Poaceae) is a perennial grass endemic to the Elbe estuary growing in tidal freshwater and oligohaline marshes. Its putative ancestor, D. cespitosa , is a holarctic distributed species, which is common and widespread in Northern Germany and found in moist (non-tidal) habitats. The high morphological similarity between the taxa is accompanied by strict habitat differentiation. Using a combined approach of molecular analyses (AFLP) and a mesocosm experiment with different hydrological regimes (waterlogging, short-term & long-term tidal flooding), we assessed the genetic and ecological differentiation between the taxa. We asked whether the adaptation of D. wibeliana to tidal flooding might be the result of natural divergent selection on ecological traits. Deschampsia wibeliana and D. cespitosa showed a distinct genetic differentiation in the AFLP analysis. Moreover, differences in the genetic structure among populations between both taxa indicated distinct landscape patterns in gene flow. Moreover, the taxa showed contrasting responses in terms of leaf traits and biomass production towards long-term tidal flooding and waterlogging, indicating adaptation to their respective habitats. There is substantial evidence for an early stage of ecological speciation in the endemic taxon D. wibeliana growing sympatrically with the widely distributed D. cespitosa . The endemism of D. wibeliana is very likely due to an adaptation to high abiotic stress in its habitat (tidal flooding). Our study may present one of the few cases of ecologically driven divergence of a locally adapted narrow neoendemic plant species. (Heydel, et al., 2017)

 

Punctuated Equilibrium

 

There was a controversy in the late 1980s in the field of biology about whether evolution occurs gradually or in occasional spurts. "Gradualism'' is the conventional wisdom and is a point of view traceable directly to Charles Darwin (1859). Although G.G. Simpson (1944) elaborated Darwin's theory to say that gradual change is observed to occur at highly variable rates, the mechanisms of evolution were agreed to be the same in spite of different rates. "Fast" evolution might produce a new species in 5000 years·, ''slow'' evolution might produce the same change in 50 million years. Some things, like horseshoe crabs, have not changed outwardly in 200 million years. But presumably, both horseshoe crabs and the rapidly evolving horse evolve the same way-by the gradual accumulation of so-called "microevoluationary" changes i.e., small changes each generation, which, with the passage of time (even 5000 years is a lot of generations for change to accumulate), result in a new species. A contrasting view has been suggested by Niles Eldredge and Stephen Jay Gould (1972; see also Gould and Eldredge, 1977; and Gould, 1980), named by its authors the ''punctuated equilibrium model."  Which indicates that organisms tend to stay the same for the most part, and then change abruptly. They say that evolution is characterized by stasis and leaps, that is, no change, then sudden change. the basis for this view was their reading of the fossil record (both are paleo-biologists), although the idea ,of "saltational evolution" has a long (Meyer, 1982)

Punctuational changed has garnered a large number of followers and is even applicable out of the biological sciences.

E Vrba (Vrba E. ) is credited with contributing the idea of  the idea of the extinction dynamic and the “turnover pulse” which became part of the punctuational theory.

Since punctuated equilibrium is concerned with the “tempo and mode” of evolution. The idea inside the punctuational stance may be used to support the unity of extinction and natural selection.

At each rungs of the phylogenic ladder where a species is expected to make a saltatory “leap”, the two processes NS and EX each contribute as a new species is selected and a former one disappears.

CONCLUSION

I have here tried to summarize very few of the available evidence on natural selection and extinction with the conviction that the two are intimately related. I have in fact gone to the extent of suggesting that we do not require two terms for both since they can be described under one. I am here suggesting this new term to be: “The Evolutionary Drive”

 

REFERENCES

Anderson, S. (1994) Areas and Endemism https://www.journals.uchicago.edu/doi/abs/10.1086/418743

Balogh, A. C., & Leimar, O. (2005). Müllerian mimicry: an examination of Fisher's theory of gradual evolutionary change. Retrieved 10 15, 2020, from https://ncbi.nlm.nih.gov/pmc/articles/pmc1560193

Baronchelli, A., Chater, N., Christiansen, M. H., Christiansen, M. H., & Pastor-Satorras, R. (2013). Evolution in a Changing Environment. PLOS ONE, 8(1), 1-8. Retrieved 6 23, 2020, from https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0052742

Barrufol, M., Schmid, B., Bruelheide, H., Chi, X., Hector, A., Ma, K., . . . Niklaus, P. A. (2013). Biodiversity Promotes Tree Growth during Succession in Subtropical Forest. PLOS ONE, 8(11). Retrieved 7 3, 2020, from https://ncbi.nlm.nih.gov/pmc/articles/pmc3841117

Bernard, L. C., Mills, M. E., Swenson, L., & Walsh, R. P. (2005). An Evolutionary Theory of Human Motivation. Genetic Social and General Psychology Monographs, 131(2), 129-184. Retrieved 6 23, 2020, from https://ncbi.nlm.nih.gov/pubmed/16779946

Biber, E. (2002). Patterns of endemic extinctions among island bird species. Ecography, 25(6), 661-676. Retrieved 10 30, 2020, from https://onlinelibrary.wiley.com/doi/abs/10.1034/j.1600-0587.2002.t01-1-250603.x

Biktashev, V. N. (2014). A simple mathematical model of gradual Darwinian evolution: emergence of a Gaussian trait distribution in adaptation along a fitness gradient. Journal of Mathematical Biology, 68(5), 1225-1248. Retrieved 10 24, 2020, from https://link.springer.com/article/10.1007/s00285-013-0669-3

Bohlin, R. (n.d.). Sociobiology: Evolution, Genes and Morality. Retrieved 6 23, 2020, from http://www.leaderu.com/orgs/probe/docs/sociobio.html

Bolhuis, J. J., Brown, G. R., Richardson, R. C., & Laland, K. N. (2011). Darwin in mind: new opportunities for evolutionary psychology. PLOS Biology, 9(7). Retrieved 6 23, 2020, from https://journals.plos.org/plosbiology/article?id=10.1371/journal.pbio.1001109

Caporael, L. R. (2001). Evolutionary Psychology: Toward a Unifying Theory and a Hybrid Science. Annual Review of Psychology, 52(1), 607-628. Retrieved 5 26, 2020, from https://annualreviews.org/doi/full/10.1146/annurev.psych.52.1.607

Charlesworth, B., & Charlesworth, D. (2009). Darwin and genetics. Genetics, 183(3), 757-766. Retrieved 9 23, 2020, from https://genetics.org/content/183/3/757

Choi, J. K., & Kim, S. C. (2007). Environmental Effects on Gene Expression Phenotype Have Regional Biases in the Human Genome. Genetics, 175(4), 1607-1613. Retrieved 6 27, 2020, from https://ncbi.nlm.nih.gov/pmc/articles/pmc1855137

Clark, W. E. (1930). The Classification of the Primates. Nature, 125(3146), 236-237. Retrieved 10 9, 2020, from https://nature.com/articles/125236b0

Colyvan, M., Linquist, S., Grey, W., Griffiths, P., Odenbaugh, J., & Possingham, H. P. (2009). Philosophical Issues in Ecology: Recent Trends and Future Directions. Ecology and Society, 14(2), 1-12. Retrieved 7 3, 2020, from https://ecologyandsociety.org/vol14/iss2/art22

Cosmides, L., & Tooby, J. (n.d.). Evolutionary Psychology: A Primer. Retrieved 6 23, 2020, from Center for Evolutionary Psychology: http://www.cep.ucsb.edu/primer.html

Crespi, B. J. (2000). The evolution of maladaptation. Heredity, 84(6), 623-629. Retrieved 10 31, 2020, from https://onlinelibrary.wiley.com/doi/abs/10.1046/j.1365-2540.2000.00746.x

Darwin|Darwin, C., & Wallace, A. R. (1859). On the Origin of Species by Means of Natural Selection, or the Preservation of Favoured Races in the Struggle for Life. Nature, 5(121). Retrieved 9 17, 2020, from http://darwin-online.org.uk/content/frameset?itemID=F373&viewtype=text&pageseq=1

Davari, M. R., Ram, M., Tewari, J. C., & Kaushish, S. (2010). Impact of agricultural practice on ecosystem services. International Journal of Agronomy and Plant Production, 1(1), 11-23. Retrieved 7 3, 2020, from https://cabdirect.org/cabdirect/abstract/20123384669

deLaplante, K. (2008). Philosophy of Ecology: Overview. Retrieved 7 3, 2020, from https://sciencedirect.com/science/article/pii/b9780080454054002470

Dercourt, J., & Paquet, J. (1985). Continental Drift and Sea-Floor Spreading. Retrieved 9 13, 2020, from https://link.springer.com/chapter/10.1007/978-94-009-4956-0_9

Dietz, K. (2005). Darwinian fitness, evolutionary entropy and directionality theory. BioEssays, 27(11), 1097–1101. Retrieved 6 20, 2020

Durand, P. M., Durand, P. M., Choudhury, R., Rashidi, A., & Michod, R. E. (2014). Programmed death in a unicellular organism has species-specific fitness effects. Biology Letters, 10(2), 20131088-20131088. Retrieved 6 23, 2020, from https://ncbi.nlm.nih.gov/pmc/articles/pmc3949379

Engels, F. (1883). Dialectics of Nature. Progress Publishers. Retrieved 6 20, 2020

Fay, J. C., Wyckoff, G. J., & Wu, C.-I. (2001). Positive and Negative Selection on the Human Genome. Genetics, 158(3), 1227-1234. Retrieved 9 20, 2020, from https://genetics.org/content/158/3/1227

Fazey, I., Gamarra, J. G., Fischer, J., Reed, M., Stringer, L. C., & Christie, M. (2010). Adaptation strategies for reducing vulnerability to future environmental change. Frontiers in Ecology and the Environment, 8(8), 414-422. Retrieved 7 3, 2020, from https://esajournals.onlinelibrary.wiley.com/doi/abs/10.1890/080215

Fisher, R. A. (1930). The Genetical Theory of Natural Selection. The Clarendon Press. Retrieved 10 31, 2020

Foster, K. R. (2009). A Defense of Sociobiology. Cold Spring Harbor Symposia on Quantitative Biology, 74, 403-418. Retrieved 6 23, 2020, from http://symposium.cshlp.org/content/74/403.short

Fox, G. A. (2005). EXTINCTION RISK OF HETEROGENEOUS POPULATIONS. Ecology, 86(5), 1191-1198. Retrieved 11 10, 2020, from https://esajournals.onlinelibrary.wiley.com/doi/pdf/10.1890/04-0594

Frank, S. A. (2011). Wright's adaptive landscape versus Fisher's fundamental theorem. arXiv: Populations and Evolution. Retrieved 11 5, 2020, from https://arxiv.org/abs/1102.3709

Giani, A. M., Gallo, G. R., Gianfranceschi, L., & Formenti, G. (2020). Long walk to genomics: History and current approaches to genome sequencing and assembly. Computational and structural biotechnology journal, 18, 9-19. Retrieved 6 18, 2020, from https://sciencedirect.com/science/article/pii/s2001037019303277

Gintis, H. (2014). Inclusive fitness and the sociobiology of the genome. Biology and Philosophy, 29(4), 477-515. Retrieved 6 23, 2020, from https://link.springer.com/article/10.1007/s10539-013-9404-0

Gomulkiewicz, R., & Holt, R. D. (1995). WHEN DOES EVOLUTION BY NATURAL SELECTION PREVENT EXTINCTION. Evolution, 49(1), 201-207. Retrieved 11 10, 2020, from https://onlinelibrary.wiley.com/doi/abs/10.1111/j.1558-5646.1995.tb05971.x

Goodman, M., Gw, M., & W, F. (1974). Primate phylogeny from the perspective of molecular systematics. Retrieved 10 9, 2020, from https://ncbi.nlm.nih.gov/pubmed/4133973

Gould, S. J. (1989). Punctuated equilibrium in fact and theory. Journal of Social and Biological Structures, 12, 117-136. Retrieved 10 30, 2020, from https://sciencedirect.com/science/article/pii/0140175089900407

Gould, S. J., & Eldredge, N. (n.d.). Punctuated equilibria: the tempo and mode of evolution reconsidered. Paleobiology, 3(2), 115–151. Retrieved 9 17, 2020

Grafen, A. (2003). Fisher the evolutionary biologist. Journal of the Royal Statistical Society, Series D, 52(3), 319–329. Retrieved 10 15, 2020

Hammerstein, P. (1996). Darwinian adaptation, population genetics and the streetcar theory of evolution. Journal of Mathematical Biology, 34(5), 511-532. Retrieved 10 24, 2020, from https://link.springer.com/article/10.1007/bf02409748

Hancock, A. M., Witonsky, D. B., Ehler, E., Ehler, E., Alkorta-Aranburu, G., Beall, C. A., . . . Rienzo, A. D. (2010). Human adaptations to diet, subsistence, and ecoregion are due to subtle shifts in allele frequency. Proceedings of the National Academy of Sciences of the United States of America, 107, 8924-8930. Retrieved 7 7, 2020, from https://pnas.org/content/107/supplement_2/8924

Heydel, F., Engels, J. G., Feigs, J. T., Vásquez, E., Rudolph, B., Rohwer, J. G., & Jensen, K. (2017). Adaptation to tidal flooding and rapid genetic divergence between a narrow endemic grass species and its widespread congener lead to an early stage of ecological speciation. Perspectives in Plant Ecology Evolution and Systematics, 27, 57-67. Retrieved 10 30, 2020, from https://sciencedirect.com/science/article/pii/s1433831916301743

Holdaway, S., & Fanning, P. C. (2010). Geoarchaeology in Australia: Understanding Human-Environment Interactions. Geological Society, London, Special Publications, 346(1), 71-85. Retrieved 7 3, 2020, from https://researchspace.auckland.ac.nz/handle/2292/6609

Ives, A. R., & Carpenter, S. R. (2007). Stability and Diversity of Ecosystems. Science, 317(5834), 58-62. Retrieved 7 3, 2020, from https://science.sciencemag.org/content/317/5834/58.full

Jablonski, D. (2005). Mass extinctions and macroevolution. Paleobiology, 31, 192-210. Retrieved 9 17, 2020, from http://geosci.uchicago.edu/pdfs/jablonski/massext05.pdf

Jenkins, D. G. (2015). Estimating ecological production from biomass. Ecosphere, 6(4), 1-31. Retrieved 7 3, 2020, from https://esajournals.onlinelibrary.wiley.com/doi/pdf/10.1890/es14-00409.1

Jenkins, D. G., & Ricklefs, R. E. (2011). Biogeography and ecology: two views of one world. Philosophical Transactions of the Royal Society B, 366(1576), 2331-2335. Retrieved 9 13, 2020, from https://ncbi.nlm.nih.gov/pmc/articles/pmc3130434

Klyve, D. (2014). Darwin, Malthus, Süssmilch, and Euler: The Ultimate Origin of the Motivation for the Theory of Natural Selection. Journal of the History of Biology, 47(2), 189-212. Retrieved 9 22, 2020, from http://sisd.net/cms/lib/tx01001452/centricity/domain/1297/darwin malthus sussmilch and euler- the ultimate origin of the motivation for the theory of natural selection.pdf

Kreager, P. (2009). Darwin and Lotka: Two Concepts of Population. Demographic Research, 21(21), 469-502. Retrieved 10 9, 2020, from http://demographic-research.org/volumes/vol21/16/21-16.pdf

Kulich, T., & Flegr, J. (2010). Effects of multiple gene control on the spread of altruism by group selection. arXiv: Populations and Evolution. Retrieved 6 23, 2020, from https://arxiv.org/abs/1002.4204

Lister, A. M. (2011). Fifty Thousand Years of Extinction. PLOS Biology, 9(11). Retrieved 9 18, 2020, from https://ncbi.nlm.nih.gov/pmc/articles/pmc3206006

Liu, Y.-S. (2013). [Revisiting Darwin's theory of heredity-Pangenesis]. Hereditas (beijing), 35(5), 680-684. Retrieved 10 18, 2020, from https://ncbi.nlm.nih.gov/pubmed/23732676

Losos, J. B., & Ricklefs, R. E. (2009). Adaptation and Diversification on Islands. Nature, 457(7231), 830-836. Retrieved 10 16, 2020, from https://nature.com/articles/nature07893

Lush, R. H. (1937). Report on the Fourth International Grasslands Congress of 1937. Retrieved 9 22, 2020, from https://dl.sciencesocieties.org/publications/jas/pdfs/1937/1/jan19370010351b

Maslin, M., Brierley, C., Milner, A. M., Shultz, S., Trauth, M. H., & Wilson, K. E. (2014). East African climate pulses and early human evolution. Quaternary Science Reviews, 101, 1-17. Retrieved 7 7, 2020, from https://sciencedirect.com/science/article/pii/s0277379114002418

McGrath, A. E. (2011). A Popular Classic: William Paley's Natural Theology (1802). Retrieved 11 13, 2020, from http://onlinelibrary.wiley.com/doi/10.1002/9781444392524.ch4/summary

McGue, M., & Bouchard, T. J. (1998). GENETIC AND ENVIRONMENTAL INFLUENCES ON HUMAN BEHAVIORAL DIFFERENCES. Annual Review of Neuroscience, 21(1), 1-24. Retrieved 6 23, 2020, from http://web.missouri.edu/~segerti/1000h/bouchardrev.pdf

Meyer, R. J. (1982). Marxism and punctuated evolution. Retrieved 10 30, 2020, from http://humboldt-dspace.calstate.edu/bitstream/handle/2148/1196/v4n2_spring_1982_006_meyer.pdf;sequence=1

Milner-Gulland, E. J. (2012). Interactions between human behaviour and ecological systems. Philosophical Transactions of the Royal Society B, 367(1586), 270-278. Retrieved 7 3, 2020, from https://ncbi.nlm.nih.gov/pmc/articles/pmc3223800

Moorad, J. A. (2013). A demographic transition altered the strength of selection for fitness and age-specific survival and fertility in a 19th century American population. Evolution, 67(6), 1622-1634. Retrieved 6 20, 2020, from https://ncbi.nlm.nih.gov/pmc/articles/pmc3675805

Murphy, E. A., & Elston, R. C. (1978). Genetic and evolutionary fitness. American Journal of Medical Genetics, 2(1), 51-79. Retrieved 6 20, 2020, from https://ncbi.nlm.nih.gov/pubmed/263582

Nelson, D. (2018). Mutualism, Commensalism, Parasitism: Types Of Symbiosis With Examples. Retrieved 7 3, 2020, from https://sciencetrends.com/comparing-examples-mutualism-commensalism-parasitism-symbiosis

Ober, C., & Vercelli, D. (2011). Gene–environment interactions in human disease: nuisance or opportunity? Trends in Genetics, 27(3), 107-115. Retrieved 7 3, 2020, from https://sciencedirect.com/science/article/pii/s0168952510002313

Olff, H., Alonso, D., Berg, M. P., Eriksson, B. K., Loreau, M., Piersma, T., & Rooney, N. (2009). Parallel ecological networks in ecosystems. Philosophical Transactions of the Royal Society B, 364(1524), 1755-1779. Retrieved 7 3, 2020, from https://royalsocietypublishing.org/doi/pdf/10.1098/rstb.2008.0222

Passey, B. H., Passey, B. H., Levin, N. E., Levin, N. E., Cerling, T. E., Brown, F. H., & Eiler, J. M. (2010). High-temperature environments of human evolution in East Africa based on bond ordering in paleosol carbonates. Proceedings of the National Academy of Sciences of the United States of America, 107(25), 11245-11249. Retrieved 7 7, 2020, from https://pnas.org/content/107/25/11245

Plesnar-Bielak, A., Skrzynecka, A. M., Prokop, Z. M., & Radwan, J. (2012). Mating system affects population performance and extinction risk under environmental challenge. Retrieved 6 23, 2020, from https://ncbi.nlm.nih.gov/pmc/articles/pmc3479737

Pyron, R. A., & Burbrink, F. T. (2012). EXTINCTION, ECOLOGICAL OPPORTUNITY, AND THE ORIGINS OF GLOBAL SNAKE DIVERSITY. Evolution, 66(1), 163-178. Retrieved 9 17, 2020, from https://onlinelibrary.wiley.com/doi/pdf/10.1111/j.1558-5646.2011.01437.x

Rabosky, D. L. (2013). Diversity-Dependence, Ecological Speciation, and the Role of Competition in Macroevolution. Annual Review of Ecology, Evolution, and Systematics, 44(1), 481-502. Retrieved 9 23, 2020, from https://annualreviews.org/doi/full/10.1146/annurev-ecolsys-110512-135800

Razeto-Barry, P., Díaz, J., & Vásquez, R. A. (2012). The Nearly Neutral and Selection Theories of Molecular Evolution Under the Fisher Geometrical Framework: Substitution Rate, Population Size, and Complexity. Genetics, 191(2), 523-534. Retrieved 10 15, 2020, from https://ncbi.nlm.nih.gov/pmc/articles/pmc3374315

Read, D. W. (1975). Primate Phylogeny, Neutral Mutations, and “Molecular Clocks”. Systematic Biology, 24(2), 209-221. Retrieved 10 9, 2020, from https://academic.oup.com/sysbio/article/24/2/209/1626434

Reed, D. H., Nicholas, A. C., & Stratton, G. E. (2007). Genetic quality of individuals impacts population dynamics. Animal Conservation, 10(3), 275-283. Retrieved 6 20, 2020, from https://zslpublications.onlinelibrary.wiley.com/doi/full/10.1111/j.1469-1795.2007.00120.x

Ronquist, F., & Sanmart, I. (2011). Phylogenetic Methods in Biogeography. Annual Review of Ecology, Evolution, and Systematics, 42(1), 441-464. Retrieved 9 13, 2020, from https://annualreviews.org/doi/full/10.1146/annurev-ecolsys-102209-144710

Siegert, R. J., & Ward, T. (2002). Evolutionary Psychology: Origins and Criticisms. Australian Psychologist, 37(1), 20-29. Retrieved 6 27, 2020, from https://aps.onlinelibrary.wiley.com/doi/abs/10.1080/00050060210001706636

Simmons, L. W. (2014). 25 years of Behavioral Ecology. Behavioral Ecology, 25(1), 1-3. Retrieved 7 3, 2020, from https://academic.oup.com/beheco/article/25/1/1/223859

Simon, D., Lin, M. T., & Pascual-Leone, A. (2002). “Nature versus nurture” and incompletely penetrant mutations. Journal of Neurology, Neurosurgery, and Psychiatry, 72(6), 686-689. Retrieved 5 26, 2020, from https://jnnp.bmj.com/content/72/6/686

Smith, C. H. (2012). Natural selection: A concept in need of some evolution? Complexity, 17(3), 8-17. Retrieved 9 17, 2020, from http://digitalcommons.wku.edu/cgi/viewcontent.cgi?article=1063&context=dlps_fac_pub

Smith, J. M. (1986). Evolutionary game theory. Physica D: Nonlinear Phenomena, 2(1), 43-49. Retrieved 9 19, 2020, from https://sciencedirect.com/science/article/pii/0167278986902320

Smithers, J., & Smit, B. (1997). Human adaptation to climatic variability and change. Global Environmental Change-human and Policy Dimensions, 7(2), 129-146. Retrieved 7 3, 2020, from https://sciencedirect.com/science/article/abs/pii/s0959378097000034

Sousa, J. A., Alpedrinha, J., Campos, P. R., & Gordo, I. (2016). Competition and fixation of cohorts of adaptive mutations under Fisher geometrical model. PeerJ, 4, 1-17. Retrieved 10 16, 2020, from https://peerj.com/articles/2256.pdf

Switek, B. J. (2010). Ancestor or Adapiform? Darwinius and the Search for Our Early Primate Ancestors. Evolution: Education and Outreach, 3(3), 468-476. Retrieved 6 19, 2020, from https://link.springer.com/article/10.1007/s12052-010-0261-x

Theunissen, B. (2012). Darwin and his pigeons. The analogy between artificial and natural selection revisited. Journal of the History of Biology, 45(2), 179-212. Retrieved 9 20, 2020, from https://ncbi.nlm.nih.gov/pubmed/22037999

Tuomainen, U., & Candolin, U. (2011). Behavioural responses to human-induced environmental change. Biological Reviews, 86(3), 640-657. Retrieved 7 3, 2020, from https://ncbi.nlm.nih.gov/pubmed/20977599

Valen, L. V. (1977). The Red Queen. The American Naturalist, 111(980), 809-810. Retrieved 11 5, 2020, from https://journals.uchicago.edu/doi/abs/10.1086/283213?journalcode=an

Veelen, M. v., Veelen, M. v., Luo, S., & Simon, B. (2014). A simple model of group selection that cannot be analyzed with inclusive fitness. Journal of Theoretical Biology, 360, 279-289. Retrieved 6 27, 2020, from https://sciencedirect.com/science/article/pii/s002251931400397x

Vilenkin, B., Chikatunov, V., Coad, B. W., & Schileyko, A. A. (2009). A random process may control the number of endemic species. Biologia, 64(1), 107-112. Retrieved 10 24, 2020, from https://link.springer.com/article/10.2478/s11756-009-0020-z

Vrba, E. S. (1983). Macroevolutionary Trends: New Perspectives on the Roles of Adaptation and Incidental Effect. Science, 221(4608), 387-389. Retrieved 11 5, 2020, from https://ncbi.nlm.nih.gov/pubmed/17798894

Walter, H. (1971). Remarks on the environmental adaptation of man. Human Genetics, 13(2), 85-97. Retrieved 7 3, 2020, from https://link.springer.com/article/10.1007/bf00295790

Went, F. W. (1973). Competition Among Plants. Proceedings of the National Academy of Sciences of the United States of America, 70(2), 585-590. Retrieved 9 22, 2020, from https://pnas.org/content/pnas/70/2/585.full.pdf

West, S. A., Griffin, A. S., & Gardner, A. W. (2008). Social semantics: how useful has group selection been? Journal of Evolutionary Biology, 21(1), 374-385. Retrieved 6 27, 2020, from https://onlinelibrary.wiley.com/doi/full/10.1111/j.1420-9101.2007.01458.x

White, T. D., Asfaw, B., Beyene, Y., Haile-Selassie, Y., Lovejoy, C. O., Suwa, G., & WoldeGabriel, G. (2009). Ardipithecus ramidus and the Paleobiology of Early Hominids. Science, 326(5949), 64-86. Retrieved 10 31, 2020, from https://science.sciencemag.org/content/326/5949/64.full

Willard, D. (n.d.). Reflections on Dawkins' The Blind Watchmaker. Retrieved 6 23, 2020, from Dallas Willard: http://www.dwillard.org/articles/artview.asp?artID=52

Wilson, D. S. (2012). The Central Question of Group Selection. Retrieved 6 27, 2020, from Edge Foundation, Inc.: http://edge.org/conversation/the-false-allure-of-group-selection

Winterhalder, B. (1980). Environmental Analysis in Human Evolution and Adaptation Research. Human Ecology, 8(2), 135-170. Retrieved 7 3, 2020, from https://link.springer.com/article/10.1007/bf01531439

Winther, R. G. (2000). Darwin on Variation and Heredity. Journal of the History of Biology, 33(3), 425-455. Retrieved 9 20, 2020, from https://link.springer.com/article/10.1023/a:1004834008068

Witt, C. C., & Maliakal-Witt, S. (2007). Why are diversity and endemism Linked on islands. Ecography, 30(3), 331-333. Retrieved 10 24, 2020, from https://onlinelibrary.wiley.com/doi/full/10.1111/j.0906-7590.2007.04837.x

Wyllie, P. J. (1974). Plate tectonics, sea-floor spreading, and continental drift: an introduction. Retrieved 9 13, 2020, from http://archives.datapages.com/data/specpubs/structu1/data/a154/a154/0001/0000/0005.htm